Exploring the Real-world Applications of Cosine Similarity
Cosine similarity is a mathematical metric used to measure the similarity between two vectors in a multi-dimensional space, particularly in high-dimensional spaces, by calculating the cosine of the angle between them.
This is our comprehensive guide on cosine similarity, an essential concept in the field of data science, text analysis, machine learning, and much more. If you've ever wondered what cosine similarity is or how it's used in real-world applications, you're in the right place.
What is Cosine Similarity?
Cosine similarity is a mathematical way to measure how similar two sets of information are. In the simplest terms, it helps us understand the relationship between two elements by looking at the "direction" they are pointing in, rather than just comparing them based on their individual values.
How does Cosine Similarity work?
Cosine similarity quantifies the similarity between two vectors by measuring the cosine of the angle between them. This is particularly useful in text analysis, where texts are converted into vectors. Each dimension of the vector represents a word from the document, with its value indicating the frequency or importance of that word.
When calculating cosine similarity, first, the dot product of the two vectors is found. This product gives a measure of how vectors in the same direction are aligned. Then, the magnitudes (or lengths) of each vector are calculated. The cosine similarity is the dot product divided by the product of the two vectors' magnitudes.
This method effectively captures the orientation (or direction) of the vectors and not their magnitude, making it a reliable measure of similarity in texts of varying lengths. It's widely used in applications like recommendation systems, document clustering, and information retrieval, where understanding the similarity or dissimilarity between texts is crucial.
A very simple example of Cosine Similarity
Imagine you're a book lover, and you've rated three books: "The Lunar Mystery," "Secrets of the Ocean," and "Flight of the Phoenix." You've rated them on a scale of 1 to 5. Your friend has also rated these same books on the same scale:
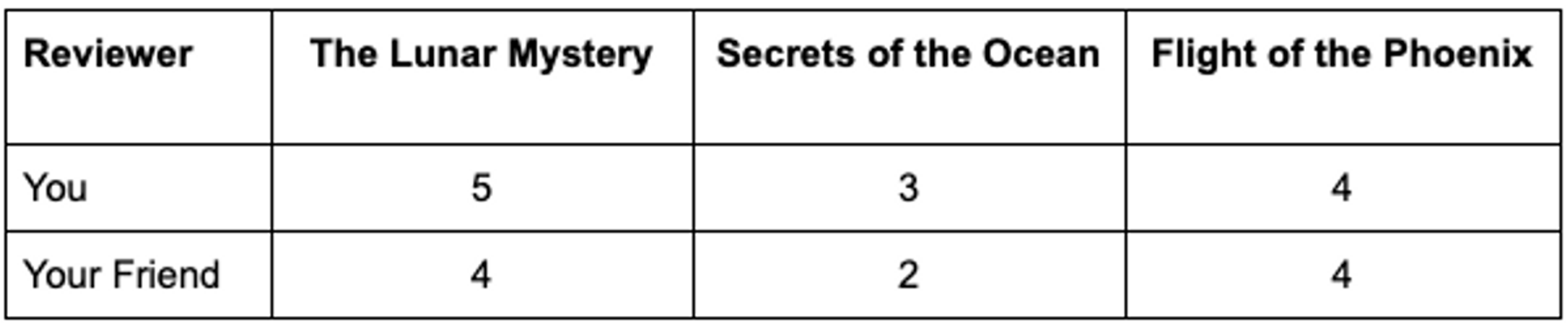
Both of your ratings can be represented as lists or, in mathematical terms, as "vectors", represented as [5,3,4] and [4,2,4].
Do you and your friend have similar ratings? You can look at the lists and come up with a qualitative “yes they’re pretty close”, or you can use cosine similarity to reach a quantitative measure! We will come back to this example, but cosine similarity is a concept that has far-reaching applications in areas like search engines, natural language processing, and recommendation systems.
The Cosine Similarity visualized
In the above example had two vectors:
- Your ratings: [5,3,4]
- Your friend's ratings: [4,2,4]
Using cosine similarity, we can quantify how similar these vectors are. The cosine similarity will return a value between -1 and 1; a value closer to 1 indicates greater similarity. In our example, calculating the cosine similarity gives us a value 0.9899, suggesting that you and your friend have very similar tastes in books. If you had another friend with ratings of [1,5,2], the cosine similarity would be 0.7230, suggesting less similar tastes.
The site math3d.org can provide a helpful way to visualize two and three-dimensional vectors. With our simple example vectors, we can see that the angle between [5,3,4] and [4,2,4] is smaller than the angle between [5,3,4] and [1,5,2]:
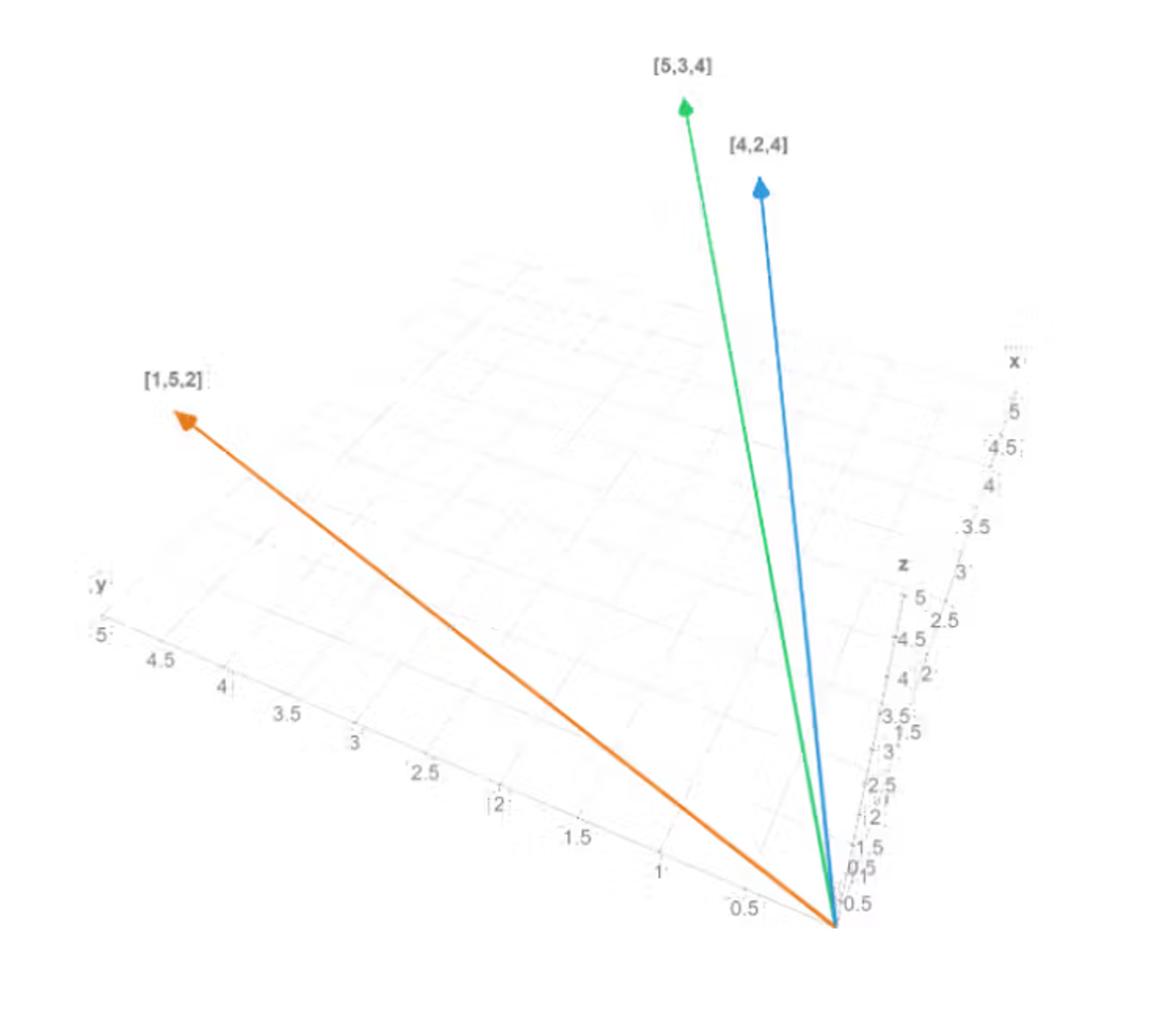
Source: https://www.math3d.org/7tCJuIQal
The mathematics of Cosine Similarity
The cosine formula used in cosine similarity offers an intuitive way to understand the relationship between two vectors. Mathematically, the cosine similarity formula is expressed as:
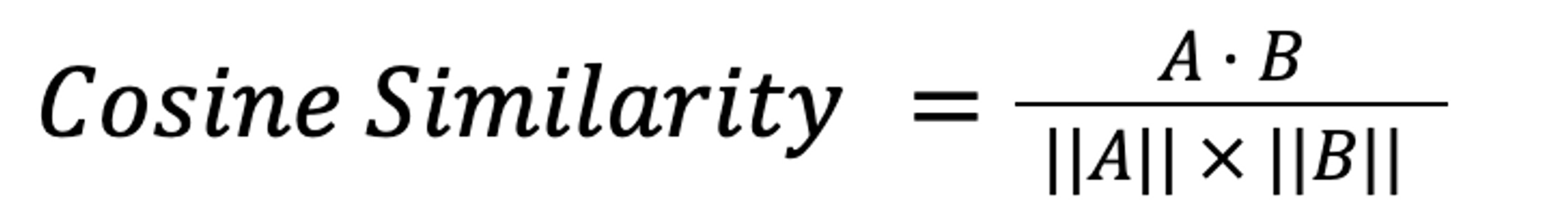
where AB is the dot product of the vectors A and B, while AB is the product of the magnitudes of the vectors A and B. This is the traditional, most compact representation of Cosine Similarity but to those without some training in linear algebra, it can be hard to understand. We will use a mathematically equivalent formula to show a way to calculate this easily.
Calculating Cosine Similarity
An alternate formulation uses more familiar sums, squares, and square roots:
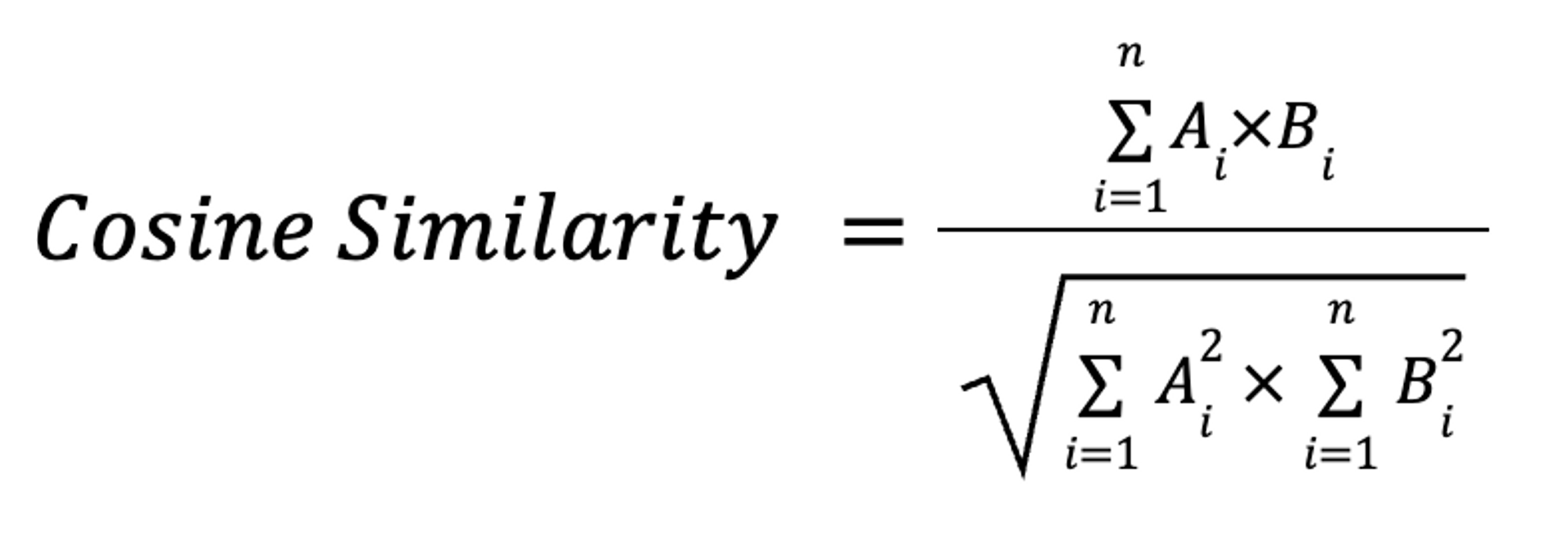
where Ai and Bi are the ith components of vectors A and B. This is how we will explain the mathematics of cosine similarity.
First is the numerator, or the dot product. To calculate this, multiply the corresponding components in each vector. For an n-dimensional vector, this would be:
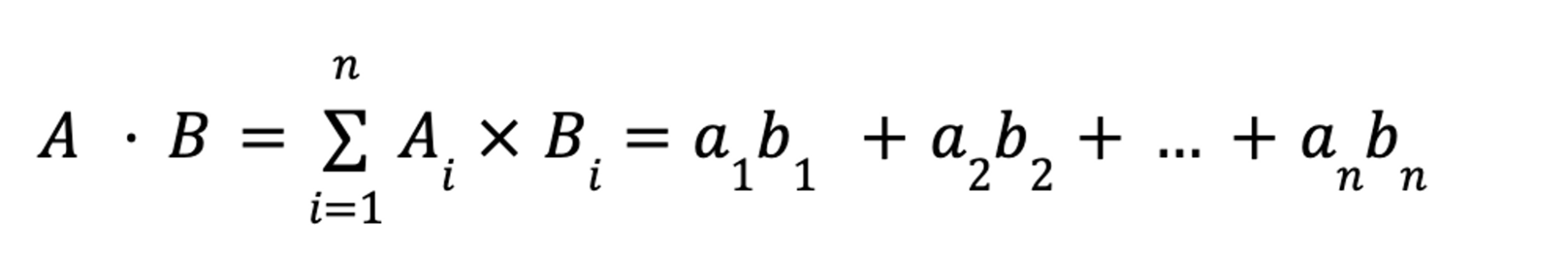
For example, our two book review vectors [5,3,4] and [4,2,4] would compute as:
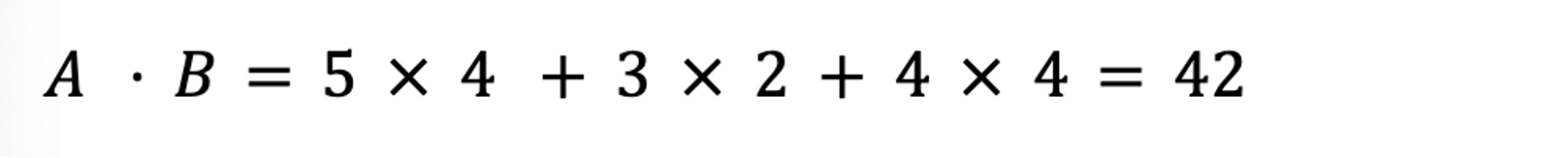
Second, the denominator, or the product of the magnitudes. Here, we compute each vector independently, and then multiply the two components:
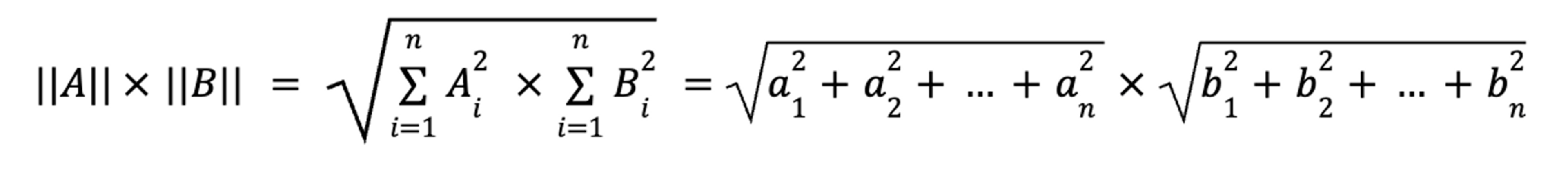
For our book review vectors:
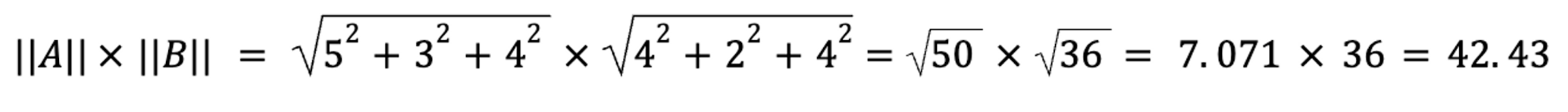
Finally, divide the second value into the first value:

And for our book review vectors:

Which means that you and your friend have reviewed the three books similarly.
In case you didn’t realize it, you’ve just done a linear algebra calculation. If it is your first, congratulations! By following these steps, you can accurately and intuitively measure the similarity between two sets of data, regardless of their size.
Why is Cosine Similarity important?
Cosine similarity is widely used in applications like natural language processing (NLP), search algorithms, and recommendation systems. It provides a robust way to understand the semantic similarity between documents, datasets, or images. For example, cosine similarity is often used in vector search engines to find the most relevant records to a given query, making search processes more efficient and precise. (Check out this guide to learn more about vector search.)
Real-world applications of Cosine Similarity
Cosine similarity is not just a theoretical concept; it has a wide range of practical applications in various domains. From simplifying searches in large datasets to understanding natural language, and from personalizing user experiences to classifying documents, cosine similarity is an indispensable tool.
Information retrieval
Cosine similarity is frequently used in information retrieval systems, such as search engines. When you enter a search query, the engine uses cosine similarity to measure the relevance of documents in its database to the query. This ensures that the most similar and relevant documents are returned, enhancing the efficiency and effectiveness of the search.
Text information is commonly embedded with simple algorithms like Bag-of-Words, or more complex trained models that are built with neural networks such as Word2Vec, GloVe, and Doc2Vec. Large Language Models (LLMs) such as GPT, BERT, LLaMa, and their derivatives are increasingly used in this space.
Text mining and natural language processing (NLP)
In text mining and NLP, cosine similarity is used to understand the semantic relationships between different pieces of text. Whether it's summarizing documents, comparing articles, or even determining the sentiment of customer reviews, this metric helps in understanding the context and content similarity among different textual data points. Different text embedding techniques like TF-IDF, Word2Vec, or BERT can be used to transform raw text into vectors that can then be compared using cosine similarity. LLMs are also widely deployed in NLP applications, particularly in the realm of autonomous agents and chatbots.
Recommendation systems
Personalization is key in today's digital experiences, and cosine similarity is a crucial component of recommendation systems that drive personalization. For example, Netflix uses cosine similarity to suggest movies based on your watching history. The system represents each movie and user as vectors and then utilizes cosine similarity to find the movies that are closest to your preferences and past viewing patterns. Embeddings are generated using techniques like Matrix Factorization or AutoEncoders.
Image processing
In image processing, cosine similarity can be used to measure the likeness between different images or shapes. Vector embeddings for images are typically generated using Convolutional Neural Networks (ConvNets or CNNs) or other deep learning techniques to capture the visual patterns in the images. This is particularly useful in facial recognition systems, in identifying patterns or anomalies in medical imaging, and in self-driving vehicles, among other applications.
Document classification
Document classification is another application where cosine similarity is invaluable. Documents can be embedded using techniques like TF-IDF or Latent Semantic Indexing (LSI, also known as Latent Semantic Analysis), and these vectors can be compared to predefined category vectors to automate document classification processes. Search engines make extensive use of this, including not only internet search engines but also domain-specific search engines such as those found in fields of law and forensics.
Clustering and data analysis
Cluster analysis is a method for grouping similar items and is often a precursor step. It's not tied to a single algorithm but employs various approaches and techniques. Cosine similarity is a popular metric used in these algorithms, thus aiding in efficiently finding clusters in high-dimensional data spaces.
Fine-tuning of the vectors is achieved by adjusting the embedding model output until a suitable data structure is revealed. The tuned embedding model can then be used as part of a real-world application.
By understanding and leveraging cosine similarity in these various domains, one can optimize processes, enhance user experiences, and make more informed decisions.
Advantages of Cosine Similarity
Cosine similarity is a widely used metric that has several advantages in various applications, such as text analysis, recommendation systems, and more. Below are some key benefits that make it a go-to choice for measuring similarity between vectors.
Scale-invariant
Cosine similarity is scale-invariant, meaning that it is not affected by the magnitudes of the vectors. This is especially useful in scenarios where you want to focus solely on the directionality of the vectors, rather than their length. Whether the values in your vector are in the tens or the millions, the cosine similarity will remain the same, making it versatile across different scales.
Dimensionality reduction
Another advantage of using cosine similarity is its compatibility with techniques like Principal Component Analysis (PCA) and t-distributed Stochastic Neighbor Embedding (t-SNE). Because it measures similarity in terms of angle rather than distance, you can reduce the dimensions of your vectors without significantly affecting the cosine similarity measure.
Simplicity and efficiency
The formula for calculating cosine similarity is straightforward, requiring just the dot product of the vectors and their magnitudes. This simplicity leads to efficient computations, making it suitable for real-time applications and large datasets.
Angle measurement
Unlike other distance-based similarity measures, cosine similarity considers the angle between vectors, providing a more intuitive sense of similarity. Smaller angles indicate higher similarity, and the measure ranges between -1 and 1, making interpretation easier.
Widely used in text analysis
Cosine similarity is particularly popular in the field of text analysis. When documents are converted into embedding vectors, cosine similarity effectively captures the "angle" between different documents, highlighting how closely the contents are related.
By considering these advantages, it becomes clear why cosine similarity is a popular choice in various machine learning and data science applications.
Potential challenges and limitations of Cosine Similarity
While cosine similarity is a valuable tool in text analysis and other applications, it comes with specific challenges and limitations that can impact its effectiveness. Understanding these challenges is crucial for accurately interpreting results and applying cosine similarity most effectively. Here are some key challenges and limitations to consider:
Handling high-dimensional data
Cosine similarity can become less effective in high-dimensional spaces, often referred to as the "curse of dimensionality". In such spaces, distinguishing between different vectors becomes challenging due to the increased distance between points.
Sensitivity to document length
While cosine similarity normalizes for document length, it can still be sensitive to variations in length. This sensitivity might affect the accuracy when comparing longer documents with shorter ones.
Interpretation of results
Interpreting the cosine similarity score requires caution. A high similarity score doesn’t always equate to high relevance or quality content, and vice versa. The context of the data and the application’s specific needs must be considered.
Dependence on vector representation
The effectiveness of cosine similarity heavily relies on the quality of the vector representation of the documents. Poorly constructed vectors can lead to inaccurate similarity measures.
Overlooking semantic meaning
Cosine similarity focuses on the frequency of terms but can overlook the deeper semantic meaning behind them. This can lead to misleading results, especially in documents where the context and semantic meaning are crucial.
Practical tips for using Cosine Similarity
To effectively utilize cosine similarity in various applications, certain practical tips can enhance accuracy and efficiency. The below tips help navigate common challenges and ensure that cosine similarity provides meaningful insights, especially in text analysis and comparison tasks.
Preprocess data
Thorough data preprocessing is crucial. This involves removing stop words which are common words that add little semantic value. Additionally, applying stemming or lemmatization helps in reducing words to their base form, thereby standardizing the dataset for better comparison.
Term weighting
Implementing TF-IDF (Term Frequency-Inverse Document Frequency) is beneficial. This technique assigns weights to each word in a document, emphasizing words that are rare across the dataset but frequent in individual documents, thereby enhancing the differentiation power of the vectors.
Consider dataset and size
The size and diversity of your dataset are critical. Larger datasets, encompassing a wide range of topics or styles, typically provide more robust and accurate similarity measures, offering a comprehensive basis for comparison.
Be mindful of computational complexity
For large datasets, the computational complexity can be significant. It's important to optimize your algorithm and computational resources to handle the data efficiently without sacrificing accuracy.
Understand the context
It’s essential to align the use of cosine similarity with the context of your application. Since cosine similarity measures the orientation rather than the magnitude of vectors, it's ideal for some scenarios (like text similarity) but may not be suitable for others where magnitude is important.
Use Cosine Similarity with Vector Search on Astra DB
Ready to put cosine similarity into practice? Vector Search on Astra DB is now available - and it does the math for you! Understand your data, derive insights, and build smarter applications today. You can register now and get going in minutes!
Cosine Similarity FAQs
What is cosine similarity?
Cosine similarity is a metric used to determine the cosine of the angle between two non-zero vectors, helping to understand the similarity between two sets of data based on orientation rather than magnitude.
How is cosine similarity calculated?
It is computed as the dot product of the vectors divided by the product of their magnitudes, with a value range of -1 to 1, where 1 indicates greater similarity.
How does cosine similarity differ from other similarity metrics?
Unlike Euclidean distance which focuses on magnitude, cosine similarity emphasizes the orientation of vectors, making it more robust in capturing pattern similarities between data sets.
Why is cosine similarity significant in natural language processing (NLP)?
It helps in comparing text to understand semantic similarity, crucial for text mining, sentiment analysis, and document clustering in NLP.
What are the advantages of using cosine similarity?
It offers a robust way to measure similarity with broad applications, especially in NLP and data analysis, and is less sensitive to the magnitude of vectors compared to other metrics.
Image Processing
In image processing, cosine similarity can be used to measure the likeness between different images or shapes. Vector embeddings for images are typically generated using Convolutional Neural Networks (ConvNets or CNNs) or other deep learning techniques to capture the visual patterns in the images. This is particularly useful in facial recognition systems, in identifying patterns or anomalies in medical imaging, and in self-driving vehicles, among other applications.
Document Classification
Document classification is another application where cosine similarity is invaluable. Documents can be embedded using techniques like TF-IDF or Latent Semantic Indexing (LSI, also known as Latent Semantic Analysis), and these vectors can be compared to predefined category vectors to automate document classification processes. Search engines make extensive use of this, including not only internet search engines but also domain-specific search engines such as those found in fields of law and forensics.
Clustering and Data Analysis
Cluster analysis is a method for grouping similar items and is often a precursor step. It's not tied to a single algorithm but employs various approaches and techniques. Cosine similarity is a popular metric used in these algorithms, thus aiding in efficiently finding clusters in high-dimensional data spaces. Fine-tuning of the vectors is achieved by adjusting the embedding model output until a suitable data structure is revealed. The tuned embedding model can then be used as part of a real-world application.
By understanding and leveraging cosine similarity in these various domains, one can optimize processes, enhance user experiences, and make more informed decisions.
The mathematics behind cosine similarity
“Complicated Math”
Previously we asked the question “Why all this complicated math?” While it might seem intuitive to simply use the angle between two vectors to measure their similarity, there are several advantages to using the cosine similarity formula:
- First, calculating the actual angle would require trigonometric operations like arccosine, which are computationally more expensive than the dot and magnitude operations in the cosine formula.
- Second, cosine similarity yields a value between -1 and 1, making it easier to interpret and compare across multiple pairs of vectors.
- Lastly, cosine similarity inherently normalizes the vectors by their magnitudes. This means it accounts for the 'length' of the vectors, ensuring that the similarity measure is scale-invariant.
So, while the angle or the Euclidean distance between the two vectors could give us some sense of similarity, the cosine similarity formula offers a more efficient and easy-to-interpret metric.
Understanding Vector Representation
In cosine similarity, the primary prerequisite is the representation of data as vectors. A vector is essentially an ordered list of numbers that signify magnitude and direction. In the context of cosine similarity, vectors serve as compact, mathematical representations of the data. For example, a document can be represented as a vector where each component of the vector corresponds to the frequency of a particular word in the document. This kind of vector representation is fundamental to the cosine similarity calculation.
The Cosine Formula and Its Intuitive Interpretation
The cosine formula used in cosine similarity offers an intuitive way to understand the relationship between two vectors. Mathematically, the cosine similarity formula is expressed as:
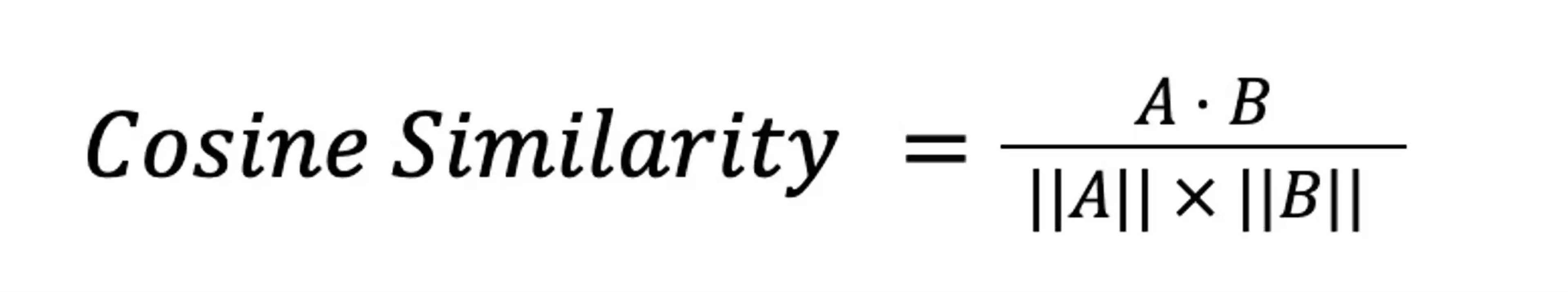
where AB is the dot product of the vectors A and B, while AB is the product of the magnitudes of the vectors A and B. This is the traditional, most compact representation of Cosine Similarity but to those without some training in linear algebra, it can be hard to understand. We will use a mathematically equivalent formula to show a way to calculate this easily.
The result of this equation is the cosine of the angle between the two vectors. An angle of 0 degrees results in a cosine similarity of 1, indicating maximum similarity. The angle between the vectors offers an intuitive sense of similarity: The smaller the angle, the more similar the vectors are. The greater the angle, the less similar they are.
Steps for Calculating Cosine Similarity
An alternate formulation uses more familiar sums, squares, and square roots:
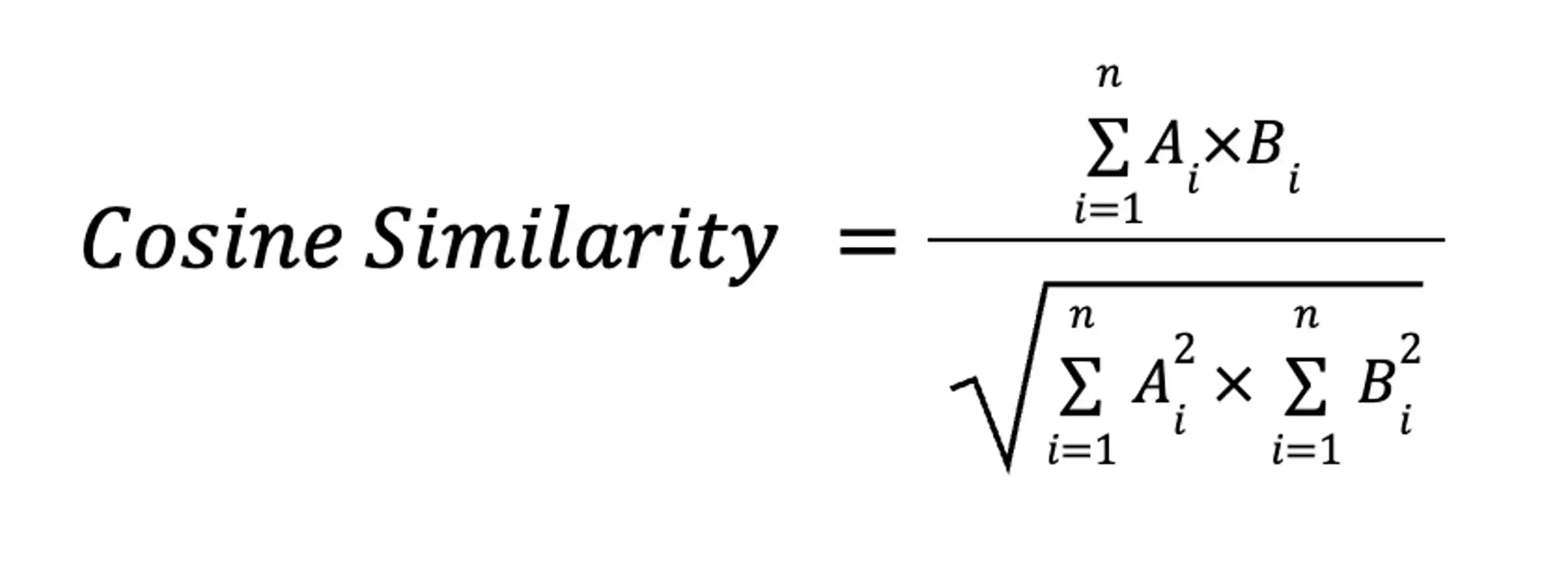
where Ai and Bi are the ith components of vectors A and B. This is how we will explain the mathematics of cosine similarity.
First is the numerator, or the dot product. To calculate this, multiply the corresponding components in each vector. For an n-dimensional vector, this would be:
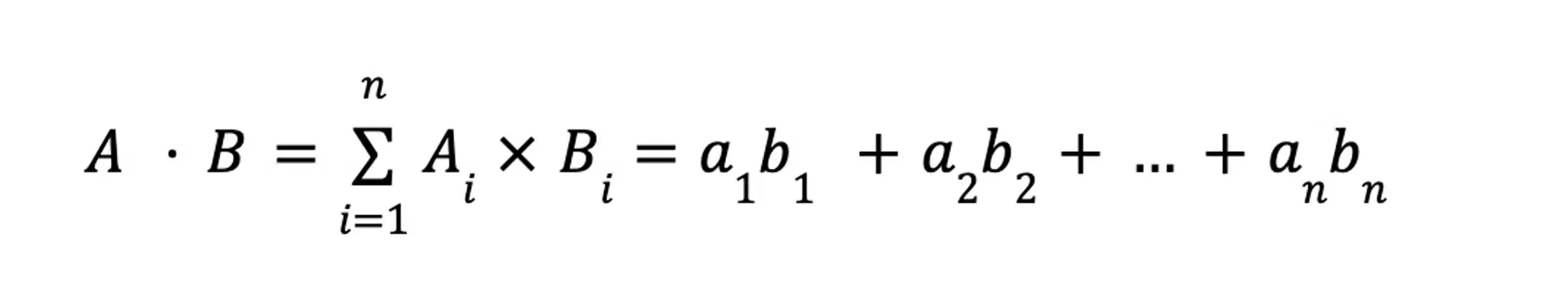
For example, our two book review vectors [5,3,4] and [4,2,4] would compute as:
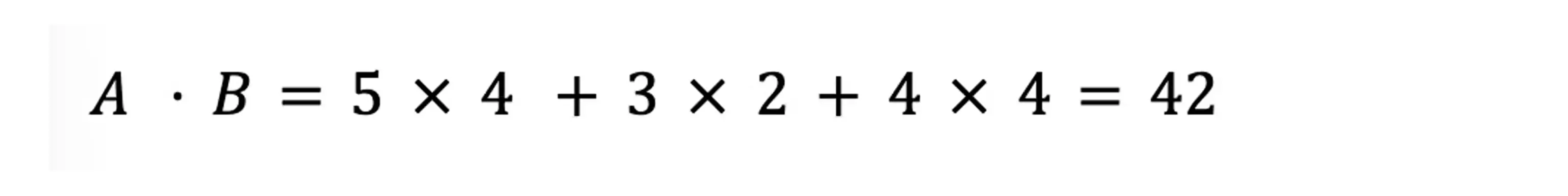
Second, the denominator, or the product of the magnitudes. Here, we compute each vector independently, and then multiply the two components:
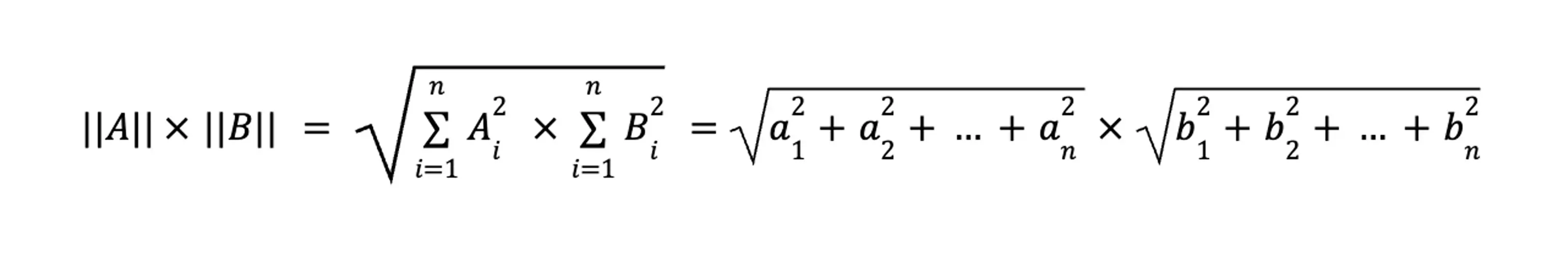
For our book review vectors:
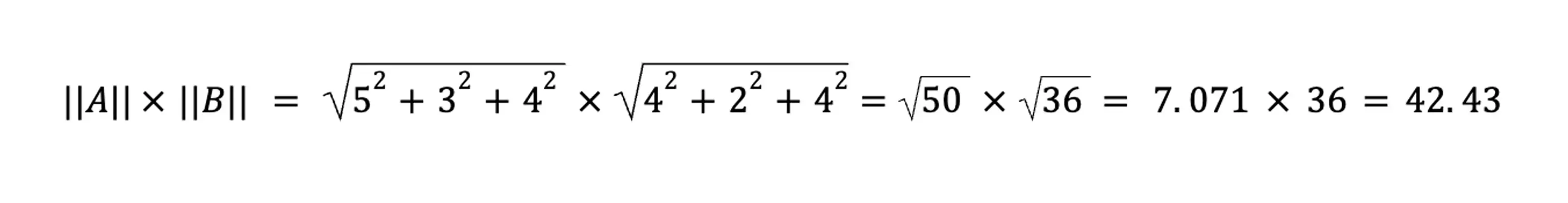
Finally, divide the second value into the first value:

And for our book review vectors:

Which means that you and your friend have reviewed the three books similarly.
In case you didn’t realize it, you’ve just done a linear algebra calculation. If it is your first, congratulations! By following these steps, you can accurately and intuitively measure the similarity between two sets of data, regardless of their size.
The “Dot Product” Cousin
Earlier, it was mentioned that there is a similarity calculation called “dot product similarity”, and that it was a close cousin to cosine similarity. Consider what would happen if all the vectors were normalized - their magnitudes would all have a value of 1. In this case, to compute the cosine similarity we could forgo the product of the magnitudes calculation - if the magnitude of each vector is 1, then 11 =1. This is the reason that many embeddings return normalized vectors - it reduces the amount of calculations that need to be performed.
Use Cosine Similarity with Vector Search on Astra DB
Ready to put cosine similarity into practice? Vector Search on Astra DB is now available - and it does the math for you! Understand your data, derive insights, and build smarter applications today. You can register now and get going in minutes!
 )
)